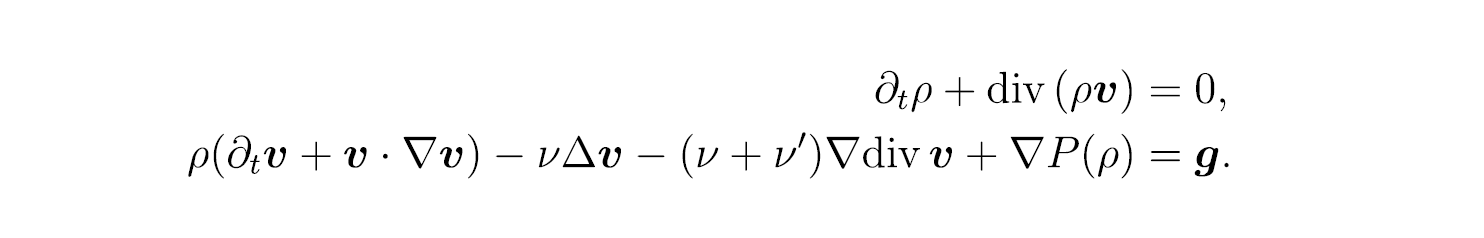可壓縮納維-斯托克斯方程中的解動力學

研究大綱

通過使用偏微分方程，可以用數學方式表達我們周圍的自然和社會現象。 其中，我正在研究可壓縮的納維-斯托克斯方程，這是一個描述流體運動的方程。 流體是一種可以流動的物質，例如水或空氣，例如，納維-斯托克斯方程適用於天氣預報。 通過分析這個方程，我們有望闡明難以捉摸的流體的行為。

研究的特點

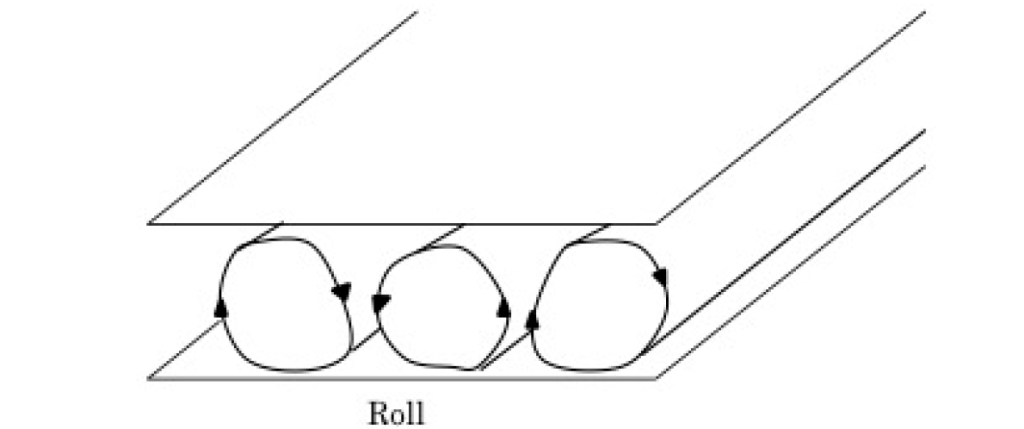
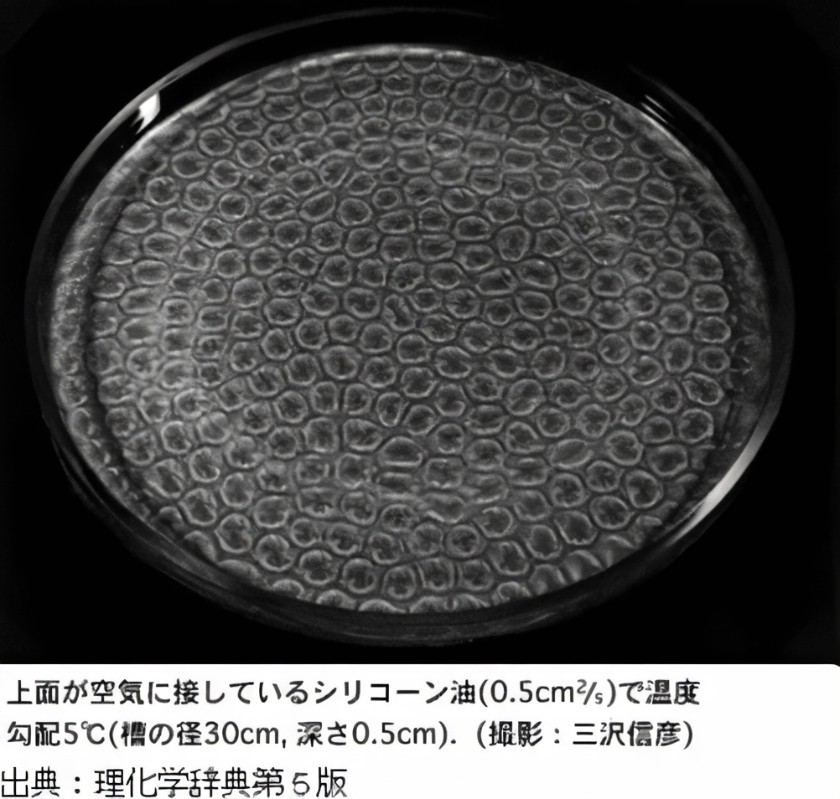
具有耗散結構的非線性偏微分方程的解以一種有趣的方式運行，無論是在數學上還是在真實的物理現象上。 與平衡態不同，耗散結構就像一種新的時空非均勻結構，由外部賦予能量而產生。 例如，當一層薄薄的流體從下方加熱時，加熱的下部流體上升到頂部，相反，上部流體向下下降，產生稱為貝納德對流的渦流。 當溫熱的味噌湯冷卻下來時，你可以看到類似的流動。

可壓縮納維-斯托克斯方程的分析不屬於傳統分析方法的框架，因為它除了涉及波傳播現象外，還涉及由於流體粘度而產生的耗散結構產生的流動模式。

研究的吸引力

可壓縮納維-斯托克斯方程是一種方程組，分為非線性方程組和雙曲線拋物面方程組。 一般來說，很難具體地顯示非線性偏微分方程的解。 但是，即使您不知道解的形狀，也可以通過充分利用方程的特性來瞭解解具有什麼樣的性質以及它的行為方式。 我認為這個領域的吸引力之一是你可以逐漸帶出解的性質，加深你對困難方程的理解。

如上所述，可壓縮納維-斯托克斯方程具有雙曲方面，因此由於波的影響，解的行為比拋物線方程（如未壓縮的納維-斯托克斯方程和擴散方程）的行為更加複雜和多樣。 因此，不可能按原樣應用已經建立的拋物線方程組的數學理論。 如果該分析方法能夠擴展到雙曲面-拋物線方程組，預計不僅對數學，而且對物理學和工程學等許多領域都有影響。

未來展望

如果我們將可壓縮納維-斯托克斯方程中稱為馬赫數的參數接近 0，我們得到未壓縮的納維-斯托克斯方程作為其極限。 由此可以預期（並非微不足道）如果馬赫數足夠小，可壓縮的納維-斯托克斯方程和未壓縮的納維-斯托克斯方程將接近。 因此，通過使用被歸類為雙曲拋物線方程的人工壓縮方程，雖然不如可壓縮的納維-斯托克斯方程強，但可以證明在一定條件下，當馬赫數較小時，解的結構與未壓縮的結構相似。 我們希望將這些結果擴展到更多情況和可壓縮性。

納維-斯托克斯方程中最大的問題是，對於三維空間中的大初始值，是否存在一個全時間和平滑的解。 它也算作克萊研究所提出的千年難題之一，許多數學家正在努力解決它。

給那些希望做這項研究的人的資訊

偏微分方程可以在數學上描述熟悉的現象，所以我認為它們有一個相對容易掌握的圖像。 但是，為了理解它，必須具備微積分和線性代數等基礎知識，以及物理和工程學的觀點。 我希望你能對各個領域感興趣，拓寬你的知識面。