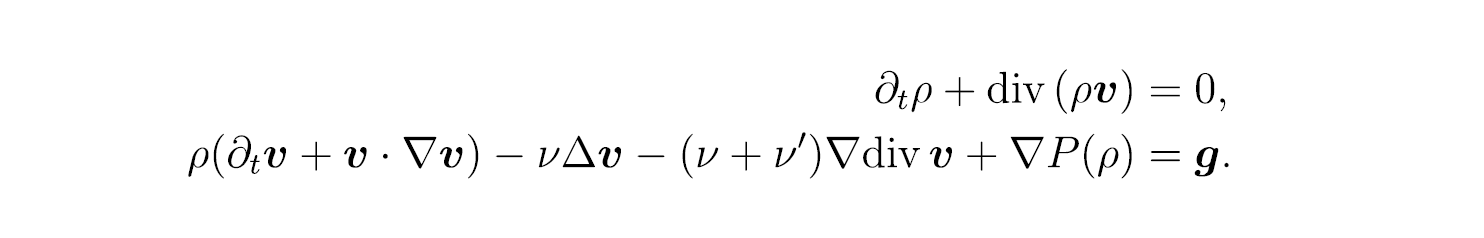可压缩 Navier-Stokes 方程中的动力学解决方案。

研究概况

偏微分方程可以用来对我们周围的自然和社会现象进行数学描述。其中，我正在研究描述流体运动的可压缩纳维-斯托克斯方程。流体是指水和空气等可以流动的物质，纳维-斯托克斯方程用于天气预报等。对这些方程的分析有望帮助阐明难以捉摸的流体行为。

研究特色

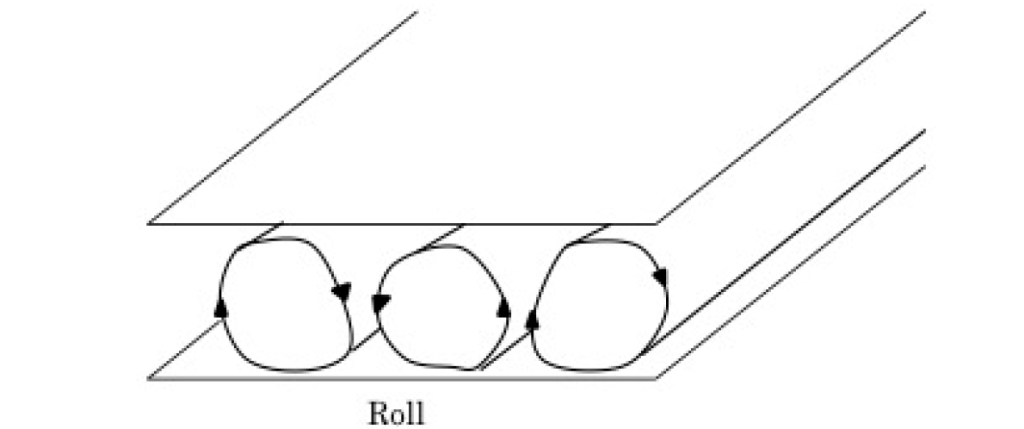
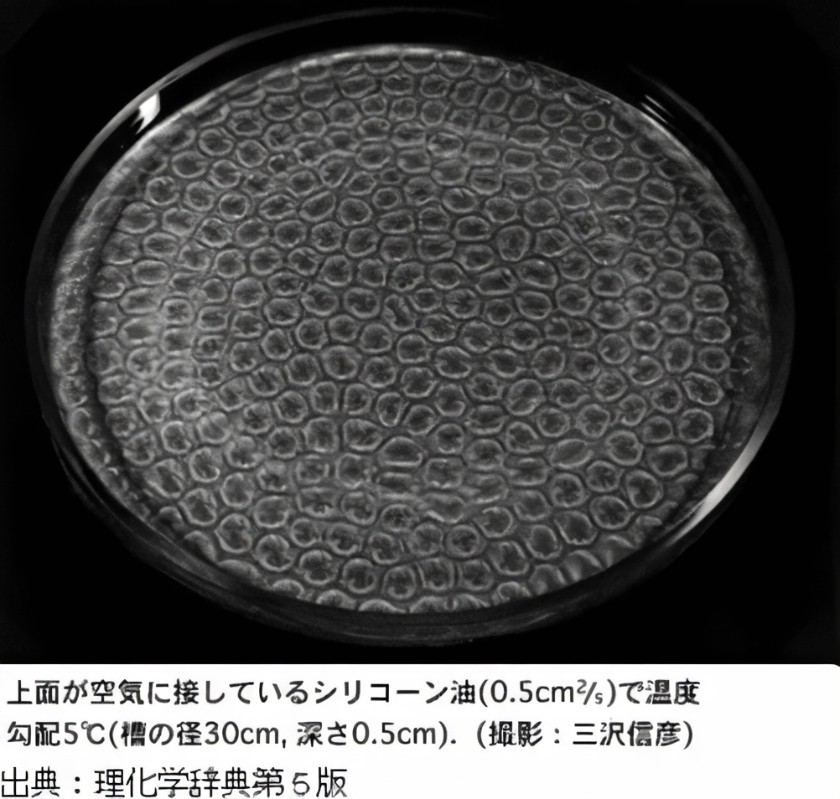
具有耗散结构的非线性偏微分方程的解在数学上和实际物理现象中都有有趣的表现。耗散结构不同于平衡状态，它是由外部能量源产生的新的非均匀时空结构。例如，当薄薄的流体层从下往上加热时，加热的下层流体向上攀升，反之亦然，导致上层流体向下下降，从而在涡旋上形成流动，这就是贝纳德对流。热酱汤冷却时也会出现类似的流动。

对可压缩 Navier-Stokes 方程的分析并不符合常规分析方法的框架，因为除了流体的粘性导致的耗散结构造成的流动模式外，它还涉及波的传播现象。

研究的吸引力

可压缩纳维-斯托克斯方程是一个方程组，分为非线性方程和双曲抛物方程。一般来说，很难将非线性偏微分方程的解以具体形式显示出来。不过，即使不知道解的形式，也可以通过充分利用方程的特性来找出解的性质和行为。我认为这一领域的魅力之一在于，即使是困难的方程，你也可以逐渐找出解的特性，加深理解。

如上所述，可压缩 Navier-Stokes 方程具有双曲特性，这使得其解的行为比抛物方程（如不可压缩 Navier-Stokes 方程或扩散方程）更加复杂多样，原因在于波的效应。因此，抛物方程系统的既有数学理论不能照搬。如果能将分析方法扩展到双曲-抛物方程系统，预计不仅会对数学产生影响，还会对物理学和工程学等许多其他领域产生影响。

前景

如果将可压缩 Navier-Stokes 方程中一个名为马赫数的参数趋近于零，则可获得作为其极限的不可压缩 Navier-Stokes 方程。由此可以预期，如果马赫数足够小，可压缩 Navier-Stokes 方程将接近不可压缩 Navier-Stokes 方程。因此，通过使用一个人造可压缩方程（它不像可压缩 Navier-Stokes 方程那样具有强烈的双曲性，但被归类为双曲-抛物线方程），证明了在某些条件下，小马赫数下的解的结构与不可压缩方程相似。我们希望能将这些结果扩展到更多情况和可压缩性情况。

此外，纳维-斯托克斯方程中最大的问题是：”对于三维空间中的大初值，是否存在一个时间全局的平滑解”。这也是克雷研究所提出的千年难题之一，许多数学家都在研究其解决方案。

给想从事这项研究的人的信息

偏微分方程可能（自私地）有一个相对平易近人的形象，部分原因是它们可以用数学方法描述人们熟悉的现象。然而，要理解它们，你不仅需要微分和积分微积分以及线性代数的基础知识，还需要物理和工程学的视角。我希望你能对各个领域产生兴趣，并拓宽自己的视野。