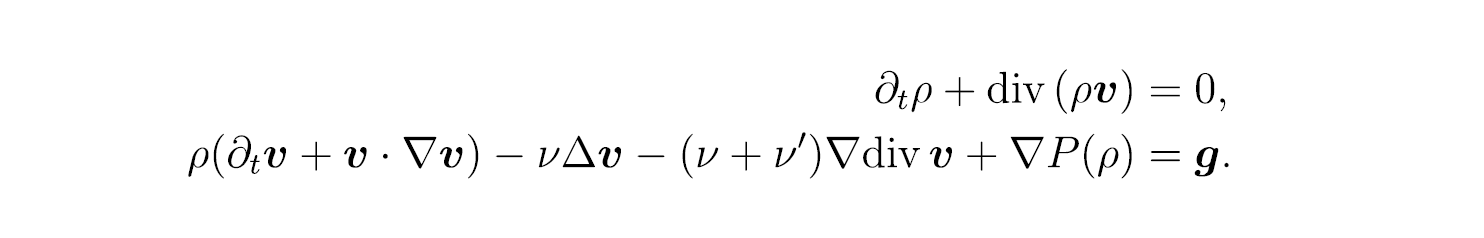‘흐름’의 수학적 분석
※게재 내용은 집필 당시의 것입니다.
압축성 Navier-Stokes 방정식에서의 해의 동역학
연구 개요
편미분방정식을 이용하면 우리 주변의 자연 현상이나 사회 현상 등을 수학적으로 표현할 수 있습니다. 그 중에서도 제가 연구하고 있는 것은 압축성 Navier-Stokes 방정식, 즉 유체의 운동을 설명하는 방정식에 대한 연구입니다. 유체란 물이나 공기와 같이 흐름을 가질 수 있는 물질을 말하는데요, 예를 들어 일기예보 등에도 Navier-Stokes 방정식이 적용되고 있습니다. 이 방정식을 분석함으로써 이해하기 어려운 유체의 거동을 규명할 수 있을 것으로 기대되고 있습니다.

연구의 특징
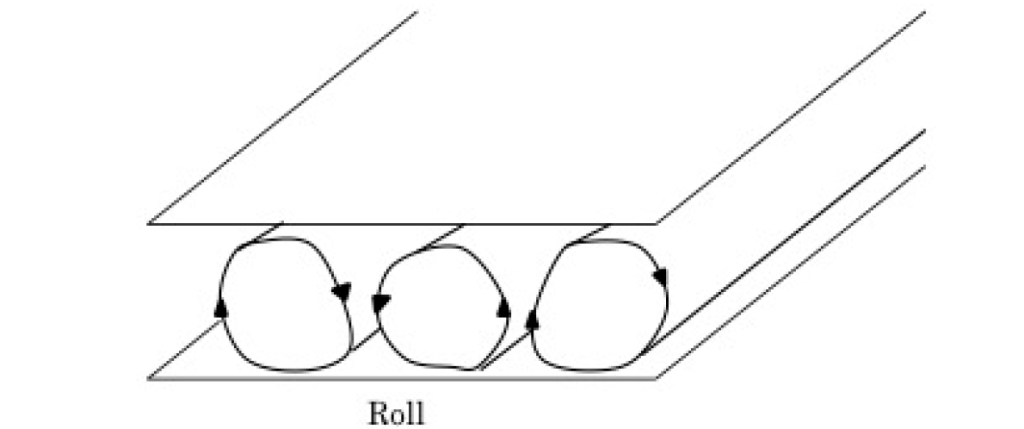
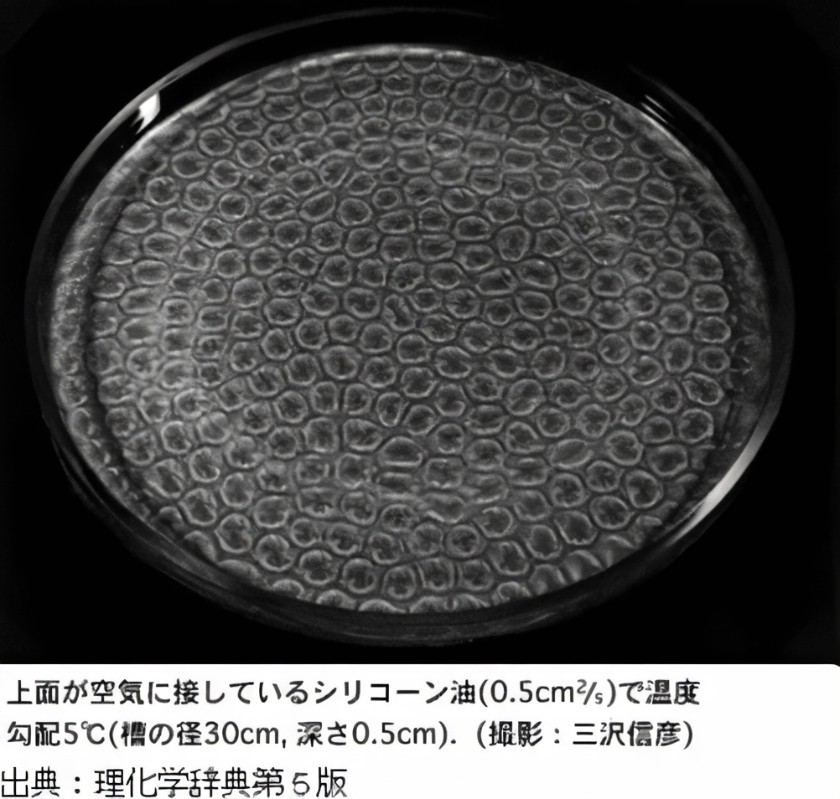
소산구조를 갖는 비선형 편미분방정식의 해는 수학적으로도, 실제 물리 현상으로도 흥미로운 거동을 보입니다. 소산 구조란 평형 상태와 달리 외부에서 에너지를 주어 새로운 시공간 비균일 구조가 만들어지는 것을 말합니다. 예를 들어, 얇은 유체층을 아래에서 가열하면 따뜻해진 아래쪽 유체가 위로 올라가고, 반대로 위쪽 유체가 아래로 내려오면서 베나르 대류라는 소용돌이 위쪽의 흐름이 발생한다. 따뜻한 된장국이 식어갈 때에도 비슷한 흐름을 볼 수 있다.
압축성 Navier-Stokes 방정식 해석은 유체의 점성에 의한 소산 구조에서 발생하는 흐름 패턴과 더불어 파동 전파 현상을 수반하기 때문에 기존 해석 방법의 틀 안에 들어가지 않습니다.
연구의 매력
압축성 Navier-Stokes 방정식은 비선형이며 쌍곡선-방정식으로 분류되는 방정식 시스템이다. 일반적으로 비선형 편미분방정식의 해를 구체적으로 표시하는 것은 어렵다고 알려져 있습니다. 하지만 해의 형태를 몰라도 방정식의 특징을 잘 활용하면 그 해의 성질이 어떤 것인지, 어떤 행동을 하는지를 알 수 있습니다. 어려운 방정식이라도 조금씩 해의 성질을 끌어내어 이해도를 높일 수 있는 것이 이 분야의 매력 중 하나라고 생각합니다.
위에서 언급한 바와 같이 압축성 Navier-Stokes 방정식은 쌍곡선적인 측면을 가지고 있기 때문에 파동의 영향으로 비압축성 Navier-Stokes 방정식이나 확산 방정식과 같은 방정식보다 해의 거동이 복잡하고 다양해진다. 따라서 방정식 시스템에 대해 확립된 수학 이론을 그대로 적용할 수 없습니다. 해석 기법을 쌍곡선-방정식 시스템까지 확장할 수 있다면, 수학뿐만 아니라 물리학, 공학 등 다양한 분야에 영향을 미칠 수 있을 것으로 기대됩니다.
향후 전망
압축성 Navier-Stokes 방정식에 포함된 마하수라는 파라미터를 0에 가까워지면 그 극한으로 비압축성 Navier-Stokes 방정식을 얻을 수 있다. 이를 통해 마하수가 충분히 작다면 압축성 Navier-Stokes 방정식과 비압축성 Navier-Stokes 방정식이 가까워질 것으로 예상할 수 있다(자명하지는 않다). 그래서 압축성 Navier-Stokes 방정식만큼 쌍곡형이 강하지는 않지만, 쌍곡-방정식 방정식으로 분류되는 인공 압축 방정식이라는 것을 이용하여, 특정 조건 하에서 마하수가 작을 경우 해의 구조가 비압축과 유사한 구조가 됨을 증명할 수 있었습니다. 이러한 결과를 더 많은 상황과 압축성의 경우로 확장할 수 있으면 좋겠다는 생각을 하고 있습니다.
또한 Navier-Stokes 방정식에서 가장 큰 문제는 ‘3차원 공간에서 큰 초기값에 대한 시공간적, 평활한 해의 존재 여부’이다. 이는 클레이 연구소가 제시한 밀레니엄 문제 중 하나로 꼽히며, 많은 수학자들이 해결을 위해 노력하고 있다.
이 연구를 희망하는 사람들에게 메시지
편미분방정식은 우리에게 친숙한 현상을 수학적으로 기술할 수 있는 것이기 때문에 비교적 쉽게 다가갈 수 있는 이미지가 있지 않을까 (제 멋대로) 생각됩니다. 하지만 이를 이해하기 위해서는 미분적분학, 선형대수 등의 기초적인 지식과 더불어 물리, 공학적인 관점도 필요합니다. 꼭 다양한 분야에 관심을 갖고 견문을 넓혀가셨으면 좋겠습니다.