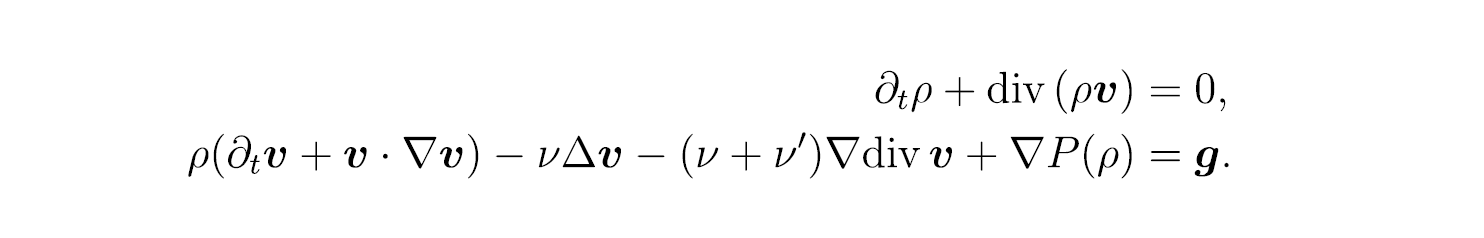圧縮性Navier-Stokes方程式における解のダイナミクス

研究の概要

偏微分方程式を用いることで、身の回りの自然現象や社会現象などを数学的に表すことができます。その中でも私が取り組んでいるのは、圧縮性Navier-Stokes方程式という、流体の運動を記述する方程式に関する研究です。流体というのは、水や空気といった流れを持ちうる物質のことで、例えば天気予報などにもNavier-Stokes方程式が応用されています。この方程式を解析することで、とらえどころのない流体の挙動を解明することができると期待されています。

研究の特色

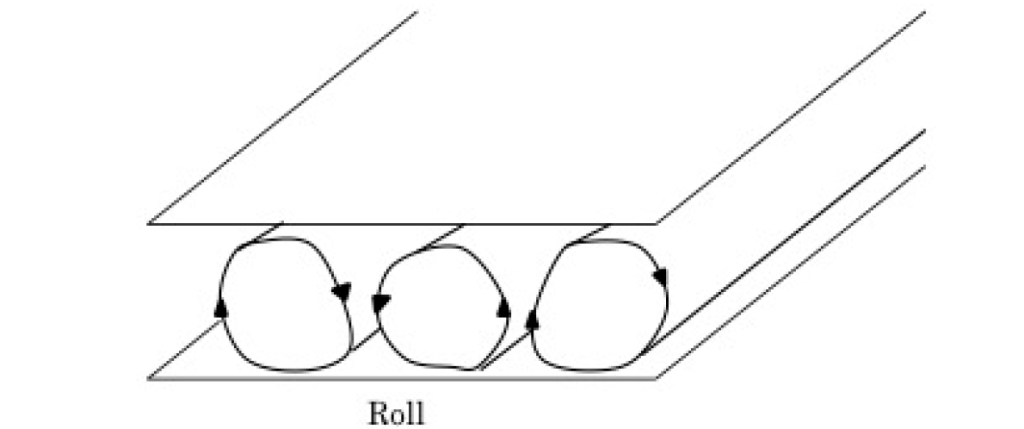
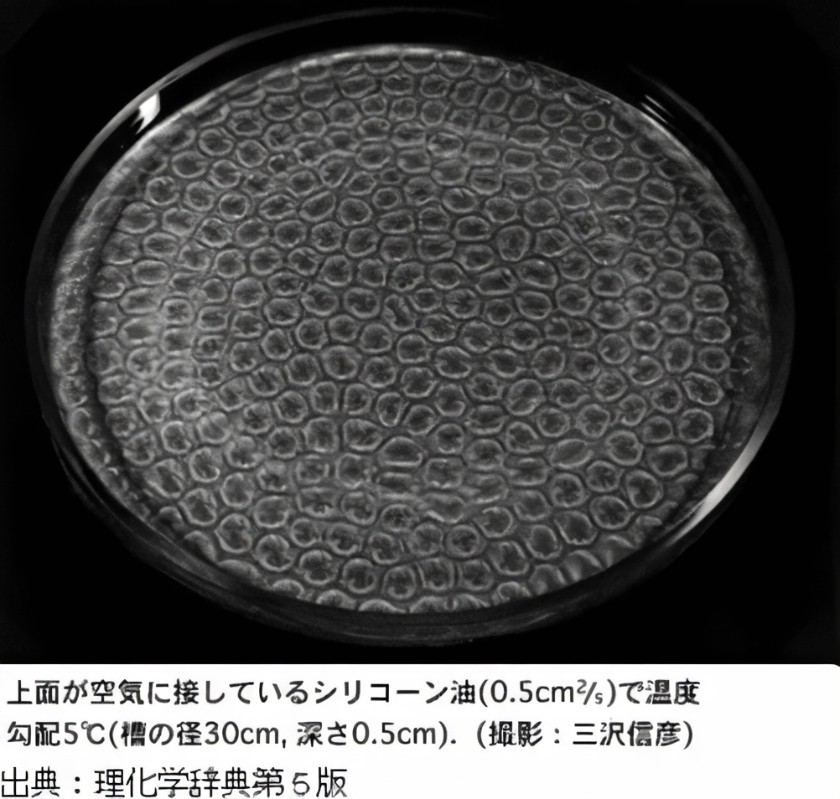
散逸構造を持つ非線形偏微分方程式の解は、数学的にも、実際の物理現象としても興味深い振る舞いをします。散逸構造というのは、平衡状態とは異なり、外部からエネルギーを与えられることによって、新たに時空非一様な構造が生まれるようなものです。例えば、薄い流体層を下から熱すると、温められた下部の流体が上に登り、逆に上部の流体が下に降りてくることで、ベナール対流と呼ばれる渦上の流れが発生します。温かいお味噌汁が冷えていくときにも、似たような流れを見ることができます。

圧縮性Navier-Stokes方程式の解析は、流体の粘性による散逸構造から生まれる流れのパターンに加えて、波の伝播現象を伴うことから、従来の解析手法の枠内には入らないものとなっています。

研究の魅力

圧縮性Navier-Stokes方程式は、非線形かつ双曲-放物型に分類される方程式系です。一般的に、非線形偏微分方程式の解を具体的に表示することは難しいとされています。ただ、解の形が分からなくても、方程式の特徴を上手く使うことで、その解がどんな性質を持っているのか、どんな振る舞いをするのかを知ることはできます。難しい方程式でも、少しずつ解の持つ性質を引き出して、理解を深めていくことができるのはこの分野の魅力の一つかなと思います。

上にも書いたように、圧縮性Navier-Stokes方程式は双曲型の側面を持つため、波の影響により、非圧縮Navier-Stokes方程式や拡散方程式といった放物型の方程式よりも、解の振る舞いは複雑かつ多様なものになります。そのため放物型方程式系に対して確立されてきた数学理論をそのまま適用することはできません。解析手法を双曲-放物型方程式系にまで拡張することができれば、数学のみならず、物理学や工学など多くの分野に影響を及ぼすことが期待できます。

今後の展望

圧縮性Navier-Stokes方程式に含まれるマッハ数と呼ばれるパラメータを0に近づけると、その極限として非圧縮Navier-Stokes方程式が得られます。このことから、マッハ数が十分小さい場合には、圧縮性Navier-Stokes方程式と非圧縮Navier-Stokes方程式とで近いものになることが予想できます（自明ではありません）。そこで、圧縮性Navier-Stokes方程式ほど双曲型が強くないものの、双曲-放物型方程式に分類される人工圧縮方程式というものを用いることで、ある条件下ではマッハ数が小さい場合に解の構造が非圧縮と似たものになることが証明できています。このような結果を、より多くのシチュエーションや圧縮性の場合にも拡張していければと考えています。

またNavier-Stokes方程式において最も大きな問題は、「3次元空間の中で大きな初期値に対する時間大域的かつ滑らかな解が存在するか」というものです。これは、クレイ研究所によって提唱されたミレニアム問題の1つにも数えられており、多くの数学者が解決に向けて取り組んでいます。

この研究を志望する方へのメッセージ

偏微分方程式は、身近な現象を数学的に記述することができるものということもあり、比較的とっつきやすいイメージがあるのかなと（勝手ながら）思っています。しかし、それを理解するためには微分積分や線形代数などの基礎的な知識の他、物理的・工学的な観点も必要になってきます。ぜひ様々な分野に興味を持って、見識を広げていってほしいと思います。