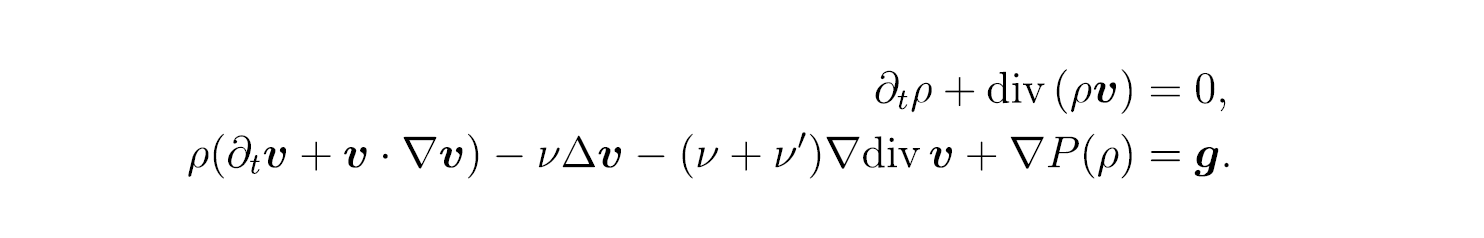Mathematical analysis of “flow”
※The content is current at the time of writing.
Solution dynamics in the compressible Navier-Stokes equations
Research Overview
Partial differential equations can be used to mathematically represent natural and social phenomena around us. Among them, I am working on the compressible Navier-Stokes equations, which describe the motion of fluids. Fluids are materials that can flow, such as water and air, and the Navier-Stokes equations are applied to weather forecasting, for example. The analysis of these equations is expected to elucidate the elusive behavior of fluids.

Research Features
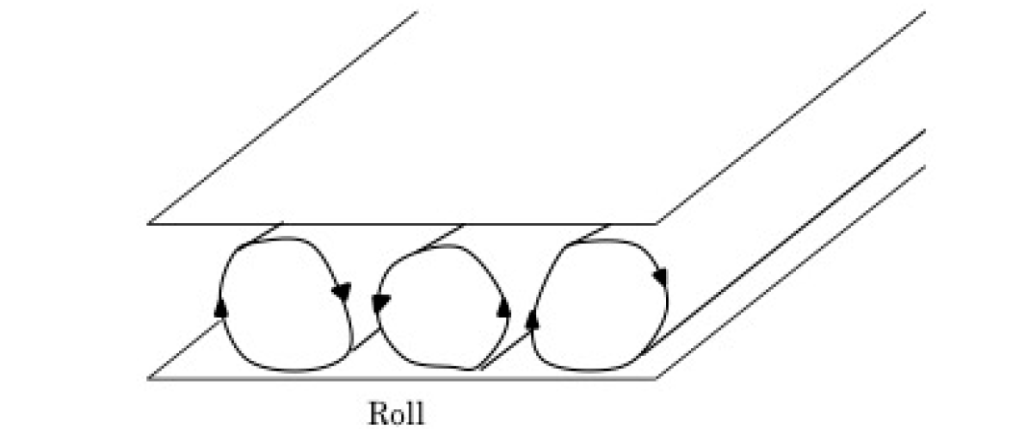
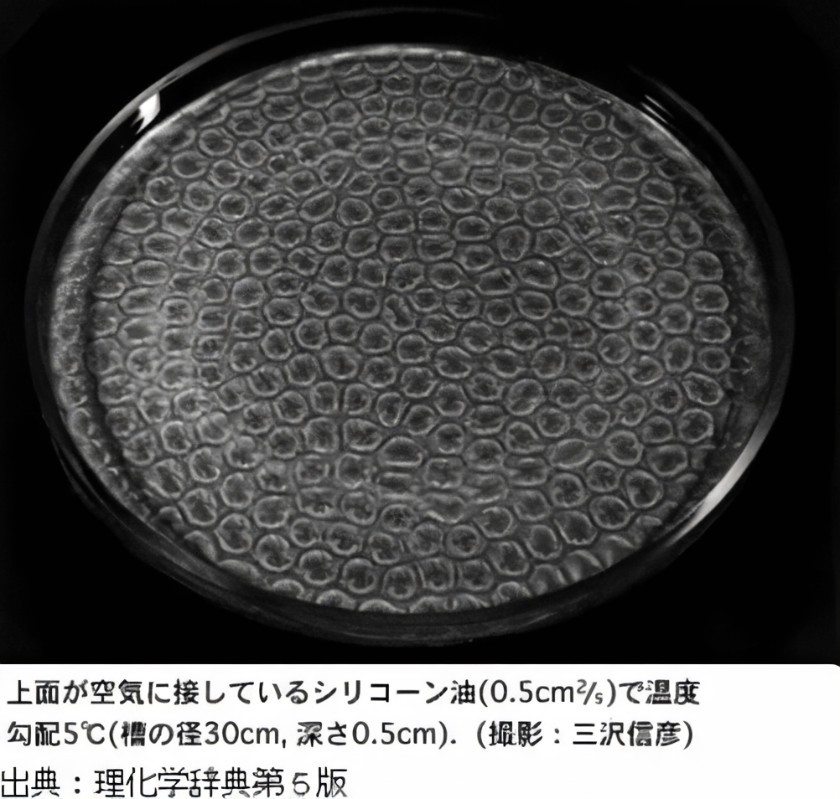
Solutions of nonlinear partial differential equations with dissipative structure behave in interesting ways, both mathematically and as real physical phenomena. Dissipative structure differs from the equilibrium state in that a new non-uniform space-time structure is created by an external source of energy. For example, when a thin fluid layer is heated from below, the warmed lower fluid climbs up, and conversely, the upper fluid descends down, creating a vortex-like flow called Benard convection. A similar flow can be seen when hot miso soup cools down.
The analysis of the compressible Navier-Stokes equations does not fit within the framework of conventional analysis methods because it involves wave propagation phenomena in addition to flow patterns resulting from dissipative structures due to the viscosity of the fluid.
Research Attraction
The compressible Navier-Stokes equations are a system of equations classified as nonlinear and hyperbolic-parabolic. In general, it is difficult to specifically display the solution of a nonlinear partial differential equation. However, even if the form of the solution is not known, it is possible to know what properties and behavior the solution has by skillfully using the characteristics of the equation. I think one of the charms of this field is that even with difficult equations, we can gradually draw out the properties of the solution and deepen our understanding.
As mentioned above, since the compressible Navier-Stokes equations have hyperbolic aspects, the behavior of their solutions is more complex and diverse than parabolic equations such as the incompressible Navier-Stokes equations or diffusion equations due to wave effects. Therefore, established mathematical theories for parabolic equations cannot be applied as they are. If analytical methods can be extended to hyperbolic-parabolic systems, it is expected to have an impact not only on mathematics but also on many other fields such as physics and engineering.
Future Outlook
If the parameter called Mach number, which is included in the compressible Navier-Stokes equations, is made close to zero, the incompressible Navier-Stokes equations are obtained as its limit. From this, we can expect that the compressible Navier-Stokes equation and the incompressible Navier-Stokes equation will be close to each other if the Mach number is sufficiently small (non-trivial). Therefore, by using an artificial compressible equation, which is classified as a hyperbolic-parabolic equation, although not as strongly hyperbolic as the compressible Navier-Stokes equation, we can prove that under certain conditions, the structure of the solution is similar to the uncompressible one for small Mach numbers. We hope to extend these results to more situations and to the case of compressibility.
Also, the biggest question in the Navier-Stokes equations is “Is there a time global and smooth solution for large initial values in 3-dimensional space? This is one of the millennium problems proposed by the Cray Institute, and many mathematicians are working on its solution.
Message to those who are interested in this research
I think (selfishly) that partial differential equations have an image of being relatively easy to approach, partly because they are capable of mathematically describing familiar phenomena. However, in order to understand them, it is necessary to have not only basic knowledge of differential and integral calculus and linear algebra, but also physical and engineering perspectives. I hope you will take an interest in a variety of fields and broaden your insight.