非線形シュレーディンガー方程式の研究
※掲載内容は執筆当時のものです。
視えない波の理解を目指して
研究の概要
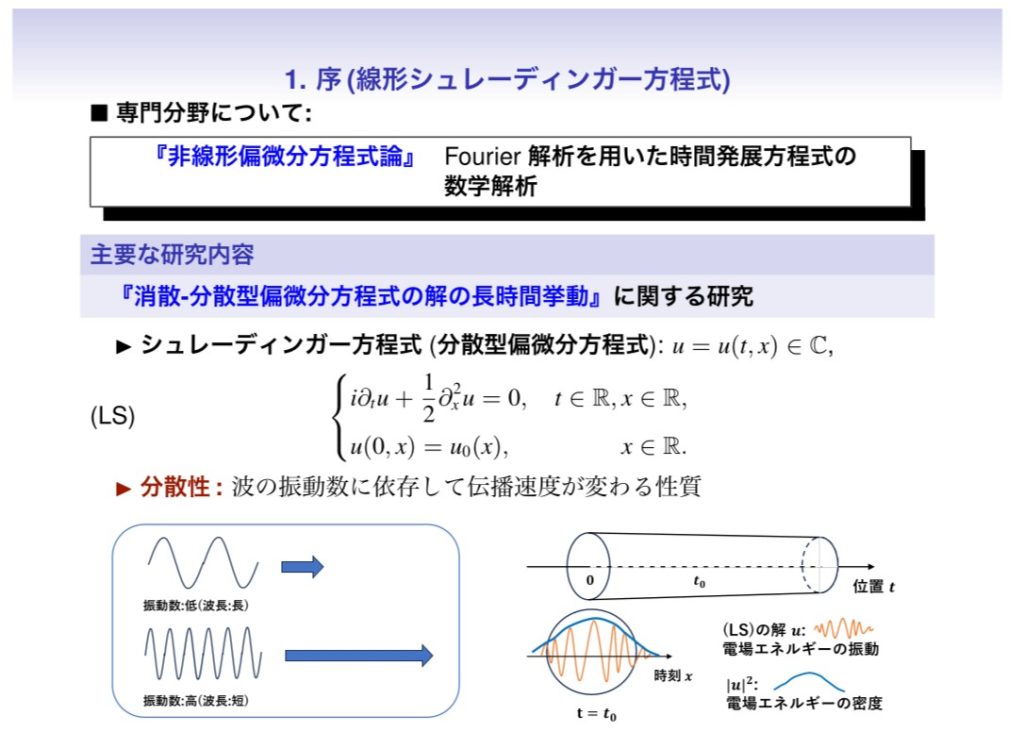
光ファイバーの中を通る電磁波は、非線形シュレーディンガー方程式という特殊な方程式に従って振る舞うことが知られています。電磁波は直接目に見えないため、その動きを理解するには、この方程式を解析することが不可欠です。非線形シュレーディンガー方程式は、波の位置と時間の2つの変数に関する微分方程式で、これを偏微分方程式と呼びます。
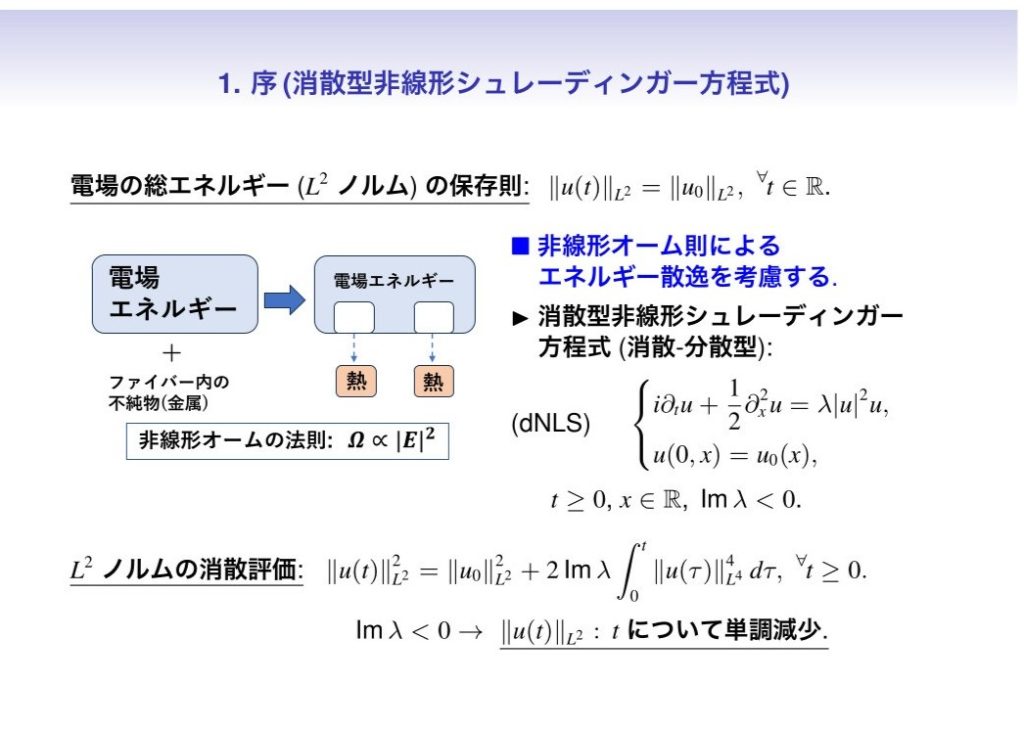
Wi-Fi通信など現代の生活に欠かせない光ファイバーでは、電磁波がファイバー内を伝播し、大量のデータを遠くまで運びます。しかし、この際に「電磁波のエネルギーを安定して遠くまで送れるか?」という重要な課題が生じます。実は、電磁波は光ファイバーに含まれる微量の金属不純物と相互作用することで、徐々にエネルギーを失ってしまうのです。
私の研究では、このエネルギー損失の程度を非線形シュレーディンガー方程式を数学的に解析することで評価し、安定した通信技術の基盤を築くことを目指しています。最近の成果として、入射する電磁波の波形によってエネルギー伝達率が変動することを数学的に明らかにしました。特に、波形がとがった成分を多く含む(パルス状の)波であるほど、より遠くまでエネルギーを運べることを証明しました。この知見が、次世代の高速・大容量通信技術の発展に貢献すれば良いなと考えています。
研究の特色
私の研究は、非線形に振る舞う複雑な波の挙動を、方程式の対称性という視点から理解することを目指しています。
光ファイバー内の電磁波の振る舞いを記述する非線形シュレーディンガー方程式は、その名の通り「非線形」な要素を含んでいます。非線形とは、簡単に言えば、波の重ね合わせを許さない性質を指します。つまり、波が複数重なったときに、それぞれの波が独立して振る舞うのではなく、互いに影響し合って形を変えてしまう性質のことです。これにより電磁波の振る舞いは非常に複雑になり、一般的にはその挙動を完全に予測することは困難です。
しかし、非線形シュレーディンガー方程式が持つ「対称性」を考慮すると、状況は大きく変わります。この「対称性」とは、方程式が持っている美しく、かつ強力な構造のことで、特定の変数変換を行っても方程式の形そのものが変わらない、という性質を指します。
この対称性こそが、複雑な非線形波動の未来の振る舞いを理解する鍵となります。特に、入射する波が「特別な形」をしている場合、この対称性を利用することで、はるか未来の振る舞いを詳細に予測できるようになります。そして、この対称性を特徴づける変数変換の数が多いほど、方程式から重要な物理情報(例えば、エネルギー保存則、質量・運動量保存則、あるいは各種有界性といった、解の振る舞いに制限を与える性質)をより多く引き出すことができます。 これらの物理的に意味のある情報を活用することで、未来の電磁波の振る舞いをコントロールし、光ファイバー通信の安定性向上に貢献することを目指しています。
研究の魅力
私の研究の魅力は、非線形シュレーディンガー方程式の解析を通して、目には見えない電磁波の振る舞いが少しずつイメージできるようになることです。最初は複雑に思える電磁波の動きも、研究が進むにつれて理解が深まり、「このような波形を持つ電磁波は、きっとこう振る舞うだろう」と、予想を立てられるようになります。そして、その予想が正しいかを、関連する物理量に着目し、微分や積分といった数学の強力なツールを駆使して、厳密に証明できることも大きな魅力です。このように、単に現象を考察するだけでなく、その背後にある普遍的な法則を数学的に捉えられる点も、面白いところだと思います。 また、この分野には多くの研究者がいます。国内外の専門家と活発に情報交換を行うことで、自分の研究内容を客観的に見つめ直したり、新たな視点を得て共同研究に発展させたりと、知的な刺激に満ちた環境で研究を進められることも、魅力の一つだと感じています。
今後の展望
非線形シュレーディンガー方程式を解析する主要な数学的ツールは、これまで不等式や微分積分といった解析学が中心で、私はこれまで、対応する物理量を微分積分し、不等式を駆使して、いかにシャープ(精密)に評価できるかという点に取り組んできました。
今後の研究では、このアプローチに加えて、新たな数学的視点を取り入れることで、さらなるブレイクスルーを目指します。特に、「不等式を使う前に、どれだけ等式変形を頑張れるか」という目標を掲げ、代数学や幾何学の解析手法も積極的に取り入れる予定です。
これにより、方程式が持つ隠れた構造をより深く理解し、これまで見過ごされてきた性質や関係性を明らかにすることで、非線形波動現象の理解を一層進展させたいと考えています。
この研究を志望する方へのメッセージ
私の研究分野では、微分積分や様々な種類の不等式といった解析学のツールを多用します。しかし、それらをただ闇雲に使うだけでは、なかなか成果には繋がりません。重要なのは、「どの物理量を微分すべきか」 を見極めたり、「どのタイミングでどの不等式を用いるか」 を適切に判断することです。 そのためには、数式の一つ一つが何を意味し、どのような役割を果たすのか、その「気持ち」を汲み取ることが大切だと感じています。研究を進める中で、まるで魔法のように現れる精巧な式変形に出会うことがあります。一見すると唐突に思えるような変形も、その背後にある数式の「気持ち」や目的を理解できれば、それは必然的なステップだったと納得できるはずです。最初はうまくいかないこともあるかもしれませんが、何度か数式と向き合ってみてください。継続が力に変わる瞬間が、きっと訪れます。


